Hello,
I am attempting to analyze a time series of .csv files. Each file corresponds to a time point. Within each file is X position, Y position, Velocity in X direction (u), Velocity in Y direction (v). The entire series of .csv files can be accessed here: Box
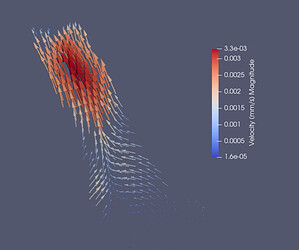
I have not used ParaView before but I have found so many helpful posts. However, detail was lacking so I decided to document my pipeline and ask how I can achieve my goal, which is to be able to select a region of the flow field and produce a Velocity (relative to flow direction) vs. Time plot. Here is what one flow field at one time point looks like:
My pipeline is as follows:

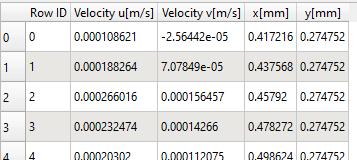
The raw .csv table looks like this (371 rows). After opening a .csv file, I learned I need to change my field delimiter to a semicolon. I am not sure about the other check boxes:

First, I convert the .csv data into point data using Table To Points filter. There is no Z dimension (2D points), so “Velocity v[m/s]” is just a place holder in this case. I selected “Keep All Data Arrays” because I need all 4 columns and I couldn’t select those I needed later on if I did not check this:
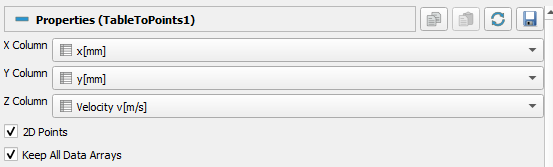
Now the new table looks like this:

What is “Points_Magnitude” and how is it useful?
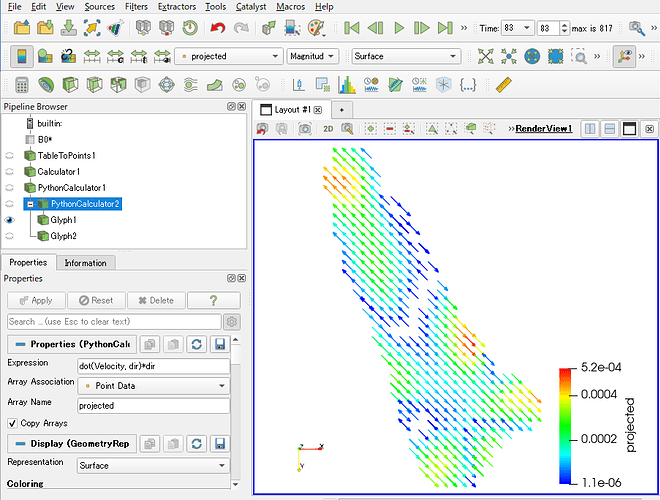
I know that I need to convert my 2 scalars (Velocity u and Velocity v) into a vector, which will result in 3 columns: X position, Y position, and the velocity vector. I use “Calculator” to multiply the scalars by iHat and jHat respectively (did I do this correctly?). I called the new values “Velocity calculate (mm/s)”:
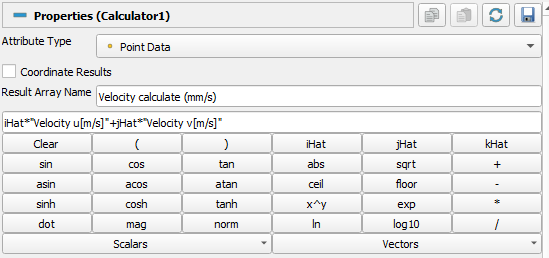
Here is the resulting table:
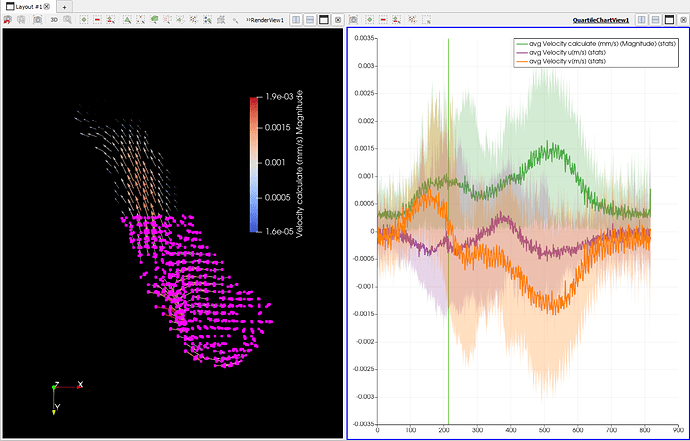
And when I use the Plot Selection Over Time filter and select part of my vector field I get this plot:
My problem is, I need to quantify velocity in the flow direction (bottom right to top left), so that I can plot negative velocity. I know I can plot over a line (but haven’t gotten that to work).
How do I 1) quantify negative velocity (relative to flow direction), 2) a specified region, and 3) over time?
Thank you for following along!