Hello All,
Is there any easy way to convert the Cartesian grid/domain to cylindrical grid/domain. I have created a Cartesian grid/domain for my simulation, to understand, analyze and compare the flow/data I want to convert this Cartesian grid/domain into cylindrical system.
Hello again,
Sorry for my unclear question, to be little more specific, I need a slice (in Cartesian grid/domain ) at an angle of 40 degree from vertical and in that slice I need to see the radial and tangential component of velocity field and need to calculate the vorticity. I follow these steps:
- To take a slice at an angle of 40 degree from the vertical axis (x normal), I modified the slice normal values as (1,-0.839,0). While considering the value -0.839 I assume that -1 is corresponding to 45 degree therefore using linear interpolation, I calculated the angle corresponding to 40 degree. Is that correct?
- To get the uradial I used the calculator: uradial=vcos(3.1440/180)+usin(3.1440/180), similarly for utheta: utheta=-vsin(3.1440/180)+ucos(3.1440/180), for getting the coordinates transformed:
r=ycos(3.1440/180)+xsin(3.1440/180) and \theta=-ysin(3.1440/180)+xcos(3.1440/180)
Now I need the vorticity in the \theta direction which is: \partial(uz)/\partial®-\partial(uradial)/\partial(z). But simultaneously I could not access the new calculated values of uradial and radial coordinate ®. Is there any way to do that? Am I on the right direction ? Any suggestion/comment will be a great help. Thanks in advance.
Sounds like a job for the Calculator ?
Hello Mathieu Westphal,
Thanks for your insight, but as I had mentioned in the previous post that “simultaneously” I need the two variables that I calculated, but at the time for doing calculations (for calculating the vorticity in \theta direction) it is showing single variable . In the previous post I had detailed my problem, could you kindly re-visit my issue. Any further comment/suggestion will be a kind help.
There is no reason that you shouldn’t be able to acess both variable after computing. Please share a screenshot.
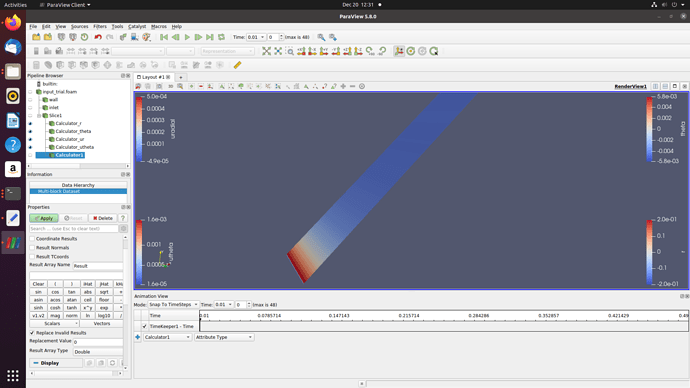
Thanks for your prompt reply, in the screenshot you can see that I calculated the variables that are required to calculate the \theta_vorticity but when I am actually trying to calculate this variable (vorticity_theta) named as Calculaotr1, I could not find them in the Scalars list. If say particularly I select the calculator_r while calculating the Calculator1 then only the variable “r” is available. hope I am clear this time about my problem.
Connect each calculator to the previous calculator instead of connecting to the slice everytime
Wow, it worked, thanks a lot. I guess it was a silly mistake from my side, I should have resolved that, sorry for bothering you. Also from the derived scalars like r, \theta, u_\radial and u_\theta I need to find out the vorticity: \partial{uz}/\partial{r}-\partial{uradial}/\partial{z}, which essentially needs the derivative of the derived quantities/scalars. Also is it possible to draw the vectors from the derived velocity fields u_radial and u_theta? Thanks again for your consistent and prompt help.
which essentially needs the derivative of the derived quantities/scalars.
Im afraid this is not easy to compute directly
Ok, thanks a lot for the clarification. Plotting the vectors out of the newly computed scalars: u_\theta and u_\radial, would be straightforward?
Sure, just use PlotData filter.
No no, sorry what I mean is that could I show the vectors representing the u_radial and u_theta, instead of the native u,v, and w?
Did you compute it ?
Sorry I didn’t understand, you mean–the vorticity or the PlotData filter or the vectors? I calculated the u_radial and u_theta and wanted to see the vectors representing the u_radial and u_theta, instead of original u, v and w. I plotted the PlotData filter using the newly calculated scalars radial, theta, u_radial, u_theta.
If you computed the u_radial and u_theta values, then you should be able to show them without any issues.